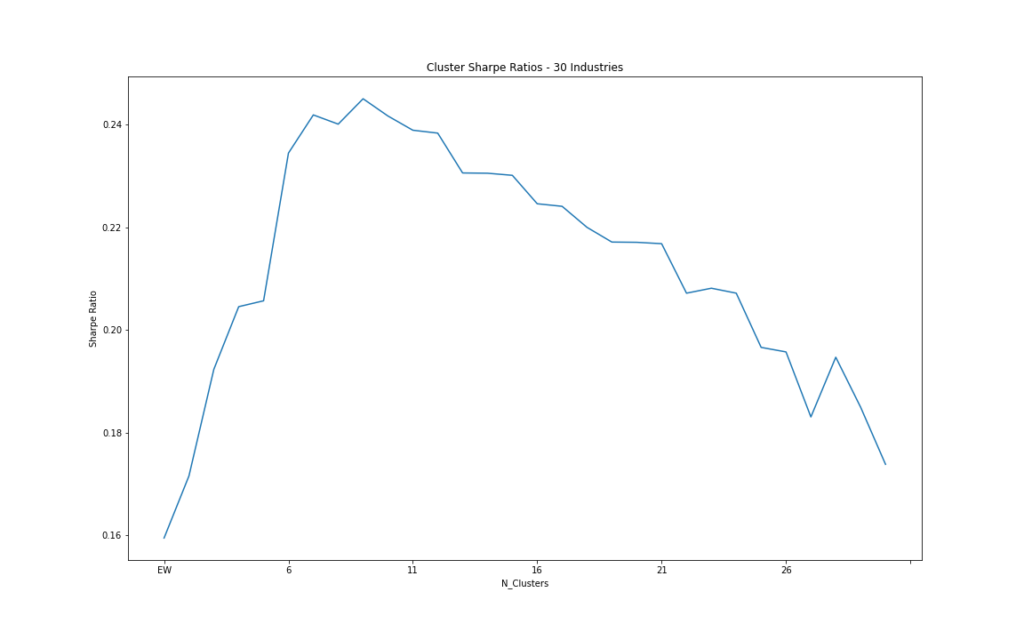
Markowitz Portfolio Optimization is haunted by estimation errors in mean and covariance estimates. Instead of optimizing the Sharpe ratio out-of-sample, the optimizers tend to maximize the estimation Error (Michaud 1989). The estimation error maximization property leads the portfolio to underperform a naïve 1/N benchmark (DeMiguel et al. (2009)), a disappointing result that questions the whole optimization task. Anyhow, there are patterns in the estimation errors that can be exploited quantitatively (Barroso & K Saxenaet (2020)). Adding to time series patterns, we find cross-sectional patterns that can be exploited to diversify estimation errors using unsupervised learning. The algorithm clusters stocks into portfolios that are then taken as inputs into the optimization process. The resulting Sharpe ratios, shifting from equal weights to the standard Markowitz portfolio show a reverted U curve.