Factor Investing: Predicting Factor Returns with Neural Networks

In the last post, I showed you cross-correlation time-series factor momentum. This strategy times factors by utilizing auto-cross-correlations in factor data (see Gupta & Kelly (2019) for a comprehensive study). This week, I will extract factor predictability from auto-cross-correlations with deep learning. I use the data of Jensen, Kelly & Pedersen (2021), which is kindly provided by Professor Bryan Kelly on his homepage. Consider we are attempting to predict the value factor using past data of highly negative/positive cross-correlated factors. With supervised machine learning, this breaks down to:

The factor i‘s (in our case i is the value factor) return ri,t+1 is predicted using last month’s returns of the driving factors j_D. A factor j is considered as a driving factor if it belongs to the highest or lowest decile of cross-correlation coefficients Ri,d. I use a simple deep neural network with 5 layers in a pyramid shape (16/8/4/2/1). The input layer uses a tanh activation function, the output layer a linear activation function. All other layers use ReLu activation. No further regularization is applied. I use factor data from January 1980 to December 1999 to train the model and data from January 2000 to December 2020 to test the data in a simple backtest. In the figure below we find the squared error of the neural network predictions compared to predictions using mean train-set returns. To rule out randomness in the initialization we repeat the prediction 50 times and keep the median as the final prediction.

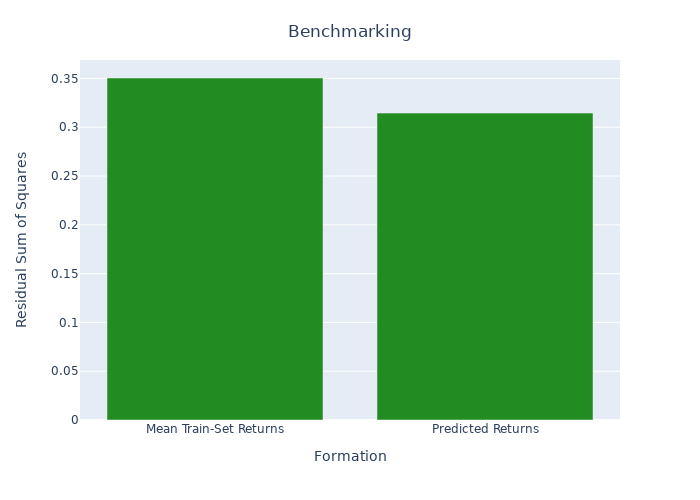
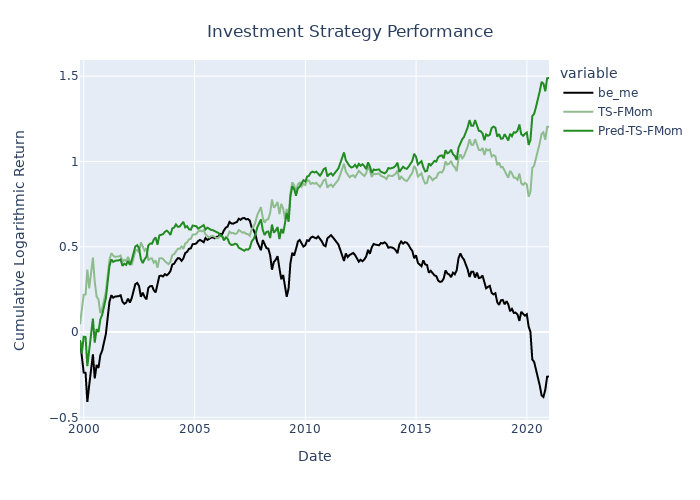
When we benchmark the predicted returns with the mean train-set returns we achieve a R2OOS of 0.103, a considerable performance. There are different applications for utilizing the predictions. Below I plot the performance of an investment strategy that uses the predicted returns, instead of prior month returns to form time-series factor momentum for the value factor. As you can see the performance is moderate in this setup.